Kinetic and Potential Energy
Kinetic and Potential Energy: Overview
This topic covers concepts, such as, Work Energy Theorem, Kinetic Energy, Calculation of Conservative Force from Potential Energy & Energy Stored in Spring etc.
Important Questions on Kinetic and Potential Energy
A satellite of mass , initially at rest on the earth, is launched into a circular orbit at a height equal to the radius of the earth. The minimum energy required is
A child is swinging a swing. Minimum and maximum heights of swing from earth’s surface are 0.75 m and 2 m respectively. The maximum velocity of this swing is:
A ball whose kinetic energy is , is projected at an angle of with the horizontal. The kinetic energy of the ball at the highest point of its flight will be,
A ball whose kinetic energy is E, is projected at an angle of to the horizontal. The kinetic energy of the ball at the highest point of its flight will be –
The potential energy of a particle as function of position is given by, where is in metre. The equilibrium position of the particle will be
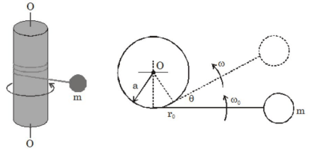
The small particle of mass is given an initial high velocity in the horizontal plane and winds its cord around the fixed vertical shaft of radius . All motion occurs essentially in the horizontal plane. If the angular velocity of the cord is when the distance from the particle to the tangency point is ., determine the angular velocity (in ) of the cord after it has turned through an angle .
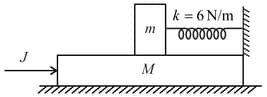
A block of mass is placed on a plank of mass , which is placed on a horizontal frictionless surface. There is no friction between the block and the plank. Block and plank are connected by a spring of spring constant as shown in the figure. An impulse is applied on the plank. Possible magnitude of acceleration of the block during its subsequent motion is/are :
A ball of mass is suspended from the ceiling with the help of an elastic cord. An additional downward force applied on the ball, if increased gradually to a value , the cord would break. What should be the additional minimum constant force that will break the cord?
Consider the potential energy given by
A rubber ball is dropped from a height of on a plane, where the acceleration due to gravity is not shown. On bouncing, it rises to . The ball loses its velocity on bouncing by a factor of . Write value of .
A object has initial velocity The total work done on the object if its velocity changes to is
If potential energy function for the force between two atoms in a diatomic molecule is approximately given by , where and are constants in standard SI units and is in metres. Find the dissociation energy of the molecule (in ). [Take and ]
The potential energy of a particle of mass , moving in the plane, is given by and being in metres. Initially at , the particle is at the origin and has velocity . Then:
A bead of mass can slide without friction on a fixed vertical loop of radius . The bead moves under the combined effect of gravity and a spring with spring constant only. The spring is rigidly attached to the bottom of the loop. Assume that the natural length of spring is zero. The bead is released from rest at with non-zero but negligible speed to the right. The gravitational acceleration is directed downward as shown in the figure. Now choose the CORRECT option(s). (Neglect any type of friction between any contact) (given )
A train with a length of moves uniformly on the horizontal section of rail road. However, the train encounters a small hill that slopes gently. With what minimum speed (in ) can the train cross the hill? The base of hill has a length , the lengths of the slope are and . The slope of hills can be consider as straight lines and the small section of rounding at the top of the hill can be ignored. Neglect air drag. (take ).

On a smooth curved track shown in the diagram, an small particle is projected from the point such that it just manages to reach the point . Assume that particle always remain contact with track. The velocity of the particle on reaching the point will be equal to :
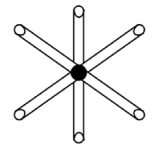
An object having its total mass concentrated at centre and having six identical rods of length each attached to it symmetrically is placed on an inclined rough surface of inclination . Object looks like a wheel with six equally spaced spokes without rim. Assume that there is no slipping and collision between the spokes and plane is perfectly inelastic and wheel always remains in the vertical plane. Also assume object remains in contact with the plane and initially center of the object is at a distance from the inclined plane and is released from rest. The acceleration due to gravity is . Pick the CORRECT statement(s) for the motion of wheel, long time after the motion has started.
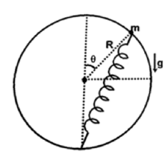
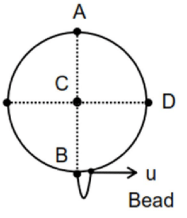
A bead of mass is threaded by a light elastic string of natural length . Initially the bead is very close to the bottom most point of a fixed vertical frictionless ring of radius and the string is slacked initially. The other end of the string is fixed to and the bead is also embedded into the ring so that it can slide along it. The elastic constant of the string is . The bead is projected from horizontally in the plane of the ring with speed . The smallest value of is for which the bead will be able to complete the circular path. The acceleration due to gravity is g. Mark the CORRECT option(s).
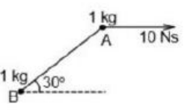
Two balls and of masses each are connected by an inextensible massless string. The system is resting on a smooth horizontal surface. An impulse of is applied to the ball A at an angle with the line joining two balls in horizontal direction as shown in the figure. Assuming that the string remains taut after impulse, if the magnitude of kinetic energy of ball is . Find the value of ''.
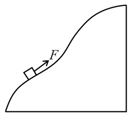
A body of mass was slowly hauled up the rough hill by a force which at each point was directed along tangent to the hill. Work done by the force